EQUAÇÃO GERAL DE GRACELI.

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

SUPERFÍCIE DE GRACELI  PARA SISTEMAS DE INFINITAS DIMENSÕES.-

  / G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

 /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

 /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

 /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

 /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

 /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

 / G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

uma função gaussiana típica usada na análise de espectros XPS: os parâmetros A₀, A₁, X_c e W são ajustados pelo programa de análise de forma que a curva ajuste-se da melhor forma possível aos dados experimentais.

ESTÁ RELACIONADA COM A SUPERFÍCIE DE FERMI. E A ENERGIA DE FERMI.

Um gás de férmions, gás de Fermi ou gás de elétrons livres é um conjunto de férmions não interativos. É a versão na Mecânica Quântica de um gás ideal, para o caso de partículas fermiônicas. Elétrons em metais e semicondutores e nêutrons em estrelas de nêutrons podem aproximadamente ser considerados gases de Fermi.

A distribuição de energia dos férmions em um gás de Fermi em equilíbrio térmico é determinada por sua densidade, pela temperatura e pelos estados de energia disponíveis, via a estatística de Fermi-Dirac. Pelo princípio de exclusão de Pauli, nenhum estado quântico pode ser ocupado por mais que um férmion, então a energia total do gás de Fermi à temperatura do zero absoluto é tão grande quanto o produto do número de partículas pelo estado de energia de cada partícula. Por esta razão, a pressão de um gás Fermi é diferente de zero na temperatura de zero absoluto, em contraste com um gás ideal clássico. Esta então chamada pressão de degenerescência estabiliza uma estrela de nêutrons (um gás de Fermi de nêutrons) ou uma estrela anã branca (um gás de Fermi de elétrons) contra a tração interna da gravidade.

É possível definir uma temperatura de Fermi abaixo do qual o gás pode ser considerado degenerado. Esta temperatura depende da massa dos férmions e da energia da densidade dos estados. Para metais, a temperatura do gás de elétrons de Fermi é geralmente de muitos milhares de kelvins, quando então eles podem ser considerados degenerados. A máxima energia dos férmions a temperatura do zero absoluto é chamada energia de Fermi. A superfície da energia de Fermi no momento espacial é chamada superfície de Fermi.

Desde que as interações são negligenciadas por definição, o problema de tratar propriedades do equilíbrio e o comportamento dinâmico de um gás de Fermi se reduz ao estudo do comportamento de partículas independentes e isoladas. Como está, é ainda relativamente tratável e dá forma ao ponto de servir de base para teorias mais avançadas (tais como a teoria do líquido de Fermi ou a teoria perturbacional) as quais levam em conta as interações com algum grau de exatidão.

Descrição matemática

Dentro da estrutura que a física estatística possibilita, segue-se que com a ajuda de conjuntos estatísticos para um número médio de ocupação ${\displaystyle \langle n_{i}\rangle }$ dos estados ${\displaystyle |i\rangle }$ com a energia ${\displaystyle E_{i}}$ da estatística de Fermi-Dirac:

${\displaystyle \langle n_{i}\rangle ={\frac {1}{e^{\frac {E_{i}-\mu }{k_{B}T}}+1}}}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Onde ${\displaystyle \mu }$ é o potencial químico, ${\displaystyle T}$ a temperatura e ${\displaystyle k_{B}}$ a constante de Boltzmann.

Estes férmions, que estão sujeitos ao princípio de exclusão de Pauli, podem estar na condição de máxima ocupação, ou seja ${\displaystyle \langle n_{i}\rangle \leq 1}$. Esta condição é que a estatística de Fermi-Dirac tratará para qualquer valor de preenchimento pleno ${\displaystyle \mu }$, porque o potencial químico de um gás ideal de Fermi não é sujeito a quaisquer restrições.

A Superfície de Fermi é definida como a superfície de energia constante ${\displaystyle \epsilon _{F}}$ no espaço recíproco. Na temperatura do zero absoluto, a superfície de Fermi separa os orbitais vazios dos orbitais ocupados. Como a corrente elétrica se deve a mudanças na ocupação dos estados próximos da superfície de Fermi, a forma e volume desta determina as propriedades elétricas de um metal. Além disso, a superfície de Fermi também é útil para determinar propriedades térmicas, magnéticas e ópticas dos metais.

Teoria

Muitas das propriedades de um material podem ser calculadas ignorando a dinâmica das interações dos elétrons entre si e com rede cristalina. Porém, existem aproximações de interações fracas entre elétrons e a rede, ou seja, assumindo que eles se movem em um potencial periódico fixo que é criado por uma rede perfeitamente rigida de íons e por uma distribuição média de elétrons.

Como estamos interessados em descrever apenas os elétrons exteriores, podemos incluir ao potencial efetivo um termo fortemente repulsivo representando o principio de exclusão de Pauli e o fato das funções de onda do núcleo e do estado de condução serem ortogonais entre si. Esse potencial é chamado de pseudopotencial e é aproximadamente zero, devido a soma do termo repulsivo e do termo atrativo, para a maior parte dos casos.

As soluções da equação de Schrodinger com um pseudopotencial fornecem o número de autoestados da partícula única, e variam continuamente com o vetor de onda k, assim elas podem ser expressas como uma sequência de funções continuas de k, ${\displaystyle \Psi _{n}(\mathbf {k,r} ),E_{n}(\mathbf {k} )}$, onde n é o número da n-ésima banda de energia.

Essas funções são periódicas no espaço recíproco, e para contar cada estado apenas uma vez, vamos nos restringir apenas à primeira zona de Brillouin. Na temperatura de zero absoluto, os elétrons em um sólido preenchem os estados de energia começando pelo estado mais baixo. O número total de elétrons determina quantas bandas disponíveis serão preenchidas com elétrons e se as últimas bandas serão preenchidas ou ficarão parcialmente vazias. Como estamos interessados em estudar os metais, vamos considerar apenas os casos onde as bandas são parcialmente preenchidas.

Se a n-ésima banda está parcialmente preenchida, os orbitais ocupados e os orbitais vazios da primeira zona de Brillouin são separados pela superfície de Fermi, que é definida como ${\displaystyle E_{n}(\mathbf {k_{F}} )=E_{F}}$, /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..onde a energia de Fermi, , é a mais alta energia para a qual existe um estado ocupado.

Um modelo simples para superfície de Fermi, o gás de elétrons livre, é obtido negligenciando os efeitos da não uniformidade do potencial sentido pelos elétrons na banda de condução. A energia de cada elétron é dada pela energia de partícula livre^[1]:

${\displaystyle E(\mathbf {k} )={\frac {\hbar ^{2}}{2m}}\mathbf {k} ^{2}}$ /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

onde estados de baixa energia ${\displaystyle E(\mathbf {k} )<E_{F}}$ preenchem uma esfera perfeita quando a temperatura é igual a zero; a superfície de Fermi é esférica. Para a maioria dos metais essa é uma ótima aproximação para a superfície de Fermi, especialmente pra metais monovalentes, onde a esfera de Fermi encontra-se totalmente na primeira zona de Brillouin.

Construção da superfície de Fermi

A Figura mostra as três primeiras zonas de Brillouin para uma rede quadrada. O circulo é uma superfície de energia constante para elétrons livres e corresponde a superfície de Fermi para um certo valor da concentração de elétrons. A área total da região ocupada por elétrons no espaço recíproco depende apenas dessa grandeza e é, portanto, independente da interação dos elétrons com a rede. No caso real a superfície de Fermi depende da interação dos elétrons com a rede e, portanto, não é um circulo perfeito.

Devido a inconveniência de se representar as regiões da superfície de Fermi que pertencem a mesma zona em diferentes partes do gráfico, utiliza-se o esquema de zona reduzido. A Figura mostra a superfície de Fermi de elétrons livres da Figura no esquema de zonas reduzido.

As regiões sombreadas representam estados ocupados por elétrons. Partes da superfície de Fermi se estendem até a segunda, terceira e quarta zonas. A quarta zona não está representada na figura, a primeira zona está totalmente ocupada.

Para passar das superfícies de Fermi de elétrons livres para elétrons quase livres de forma quantitativa é necessário a realização de complexos cálculos matemáticos, porém existe uma uma maneira qualitativa de se prever as formas das superfícies de Fermi para elétrons quase livres, levando em consideração os seguintes fatos:

• A interação do elétron com o potencial periódico da rede dá origem a zonas proibidas nos limites da zona de Brillouin.
• Quase sempre a superfície de Fermi intercepta os limites das zonas perpendicularmente.
• O potencial da rede arredonda os vértices das superfícies de Fermi.
• O volume total contido na superfície de Fermi não depende dos detalhes da interação com a rede, mas depende quase exclusivamente da concentração de elétrons.

As superfícies de Fermi para elétrons livres podem ser construídas usando o método de Harrison. Nele são determinados os pontos de rede reciproca e uma esfera de elétrons livres, de raio apropriado para a concentração de elétrons, é traçada com centro em cada um desses pontos. Qualquer ponto do espaço reciproco que esteja no interior de pelo menos uma esfera corresponde a um estado ocupado na primeira zona. Os pontos que estão no interior de pelo menos duas esferas correspondem a estados ocupados da segunda zona e assim por diante.

Medidas experimentais envolvendo a superfície de Fermi

A superfície de Fermi nos metais é uma prova de que os elétrons no sistema podem ser tratados através da teoria de quase-partículas.

Foi analisado nas seções anteriores que esta superfície é crucial para o entendimento de propriedades térmicas, magnéticas, elétricas e ópticas. Neste sentido, experimentalmente é necessária a existência de ferramentas específicas de modo a elucidar quais os materiais existentes ou mesmo descobrir quais são os formatos da superfície de fermi de determinado composto.

Neste sentido, existem diversas técnicas, como a aplicação do efeito De Haas-van Alphen Effect entre outras que pautam pela utilização de altos campos magnéticos para que ocorra a diferenciação de períodos de oscilação e assim possa-se medir indiretamente o modo com o qual os estados ocupados do material e portanto podendo inferir na superfície de Fermi.

Atualmente, duas técnicas tem tido destaque para se resolver as superfícies de fermi: ARPES, espectroscopia de fotoemissão angularmente resolvida, e STM, microscópio de tunelamento.

ARPES - Espectroscopia de fotoemissão resolvida em ângulo

An Experimental Setup of Angle-Resolved Photoemission Spectroscopy

A técnica ARPES é baseada no efeito fotoelétrico, explicado em 1905 por Einstein através do conceito de quanta de energia.

Neste efeito, os elétrons de um material podem absorver um fóton e serem ejetados se a energia do respectivo fóton é maior que a função trabalho do material.

O ARPES funciona da seguinte forma: Uma linha de radiação branca é produzida, através da utilização de um monocromador uma determinada linha é selecionada, esse comprimento de onda é então iluminado em uma amostra. Um detector então analisa os fotoelétrons emitidos pela amostra registrando a energia e o ângulo de incidência do feixe. As resoluções atuais são de aproximadamente 2 meV e 0,2° em sofisticados experimentos feitos em síncrotrons ao redor do mundo.

${\displaystyle \hbar k_{i||}=\hbar k_{f||}={\sqrt {2mE}}sin\theta }$ /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

${\displaystyle k_{iT}={\frac {1}{\hbar }}{\sqrt {2m(E_{f}cos^{2}\theta +V)}}}$ /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Ao se registrar os ângulos e as energias, é possível através da conservação de energia e do momento da onda nas direções paralela e perpendicular, registrar o valor de V0 que é a distância da energia de Fermi ao nível do vácuo. Fazendo-se um mapa para diversos vetores de onda k, é possível construir um mapa da superfície de Fermi.

Uma das maiores desvantagens da técnica ARPES é a falta de uma informação da superfície de fermi do material como um todo, pois somente é possível a análise de determinadas direções de uma só vez, e devido ao tempo de aquisição das medidas, não é possível garantir que as distribuições eletrônicas permaneçam constantes por longos intervalos temporais.

STM - Microscopia de tunelamento

A microscopia de tunelamento, uma técnica com capacidade de imageamento em espaço real, com poder de resolução atômica de superfícies. O STM funciona através da varredura de uma ponta sobre uma amostra. Através da análise da corrente de tunelamento, é possível obter uma espécie de topografia de seu material.

Diferentemente do que ocorre com o ARPES, onde é possível a análise da superfície de fermi, pode-se analisar um determinado material como todo.

Para isso, é necessária a introdução do material a ser analisado dentro de uma outra amostra conhecida. Através da utilização da sobreposição das funções de onda da amostra e da ponta e da regra de ouro de Fermi, foi notado que se o material a ser investigado tem simetria diferente da esférica na superfície de Fermi, como é o caso do Au, Cu e Ag, o espalhamento da onda de tunelamento medida pela ponta será no espaço recíproco (feito através de transformada de Fourier) será a medida da superfície de Fermi de seu material.

Um exemplo de uma superfície de Fermi obtida através do STM é a indicada na Figura, em que é possível visualizar como seria a densidade de estados ocupados de um átomo de cobalto em uma amostra de cobre.

A Energia de Fermi é a energia do nível ocupado mais energético em um sistema quântico fermiônico à temperatura de zero absoluto. A definição estende-se também a sistemas acima do zero absoluto, caso em que a energia de fermi corresponde à energia obtida mediante uma média das energias dos níveis quânticos com probabilidade de ocupação - devido à agitação térmica - diferentes da unidade, cada qual ponderado pela respectiva probabilidade de ocupação. Associa-se via de regra à energia de fermi a notação E_F, e a nomenclatura retrata nítida homenagem ao físico ítalo-americano Enrico Fermi.

Introdução

Contexto geral

A energia de Fermi é importante na hora de entender o comportamento de partículas fermiônicas, como por exemplo os elétrons. Os férmions são partículas de spin semi-inteiro para as quais verifica-se a validade do princípio de exclusão de Pauli - que dita que dois férmions idênticos não podem ocupar simultaneamente o mesmo estado quântico. Desta maneira, quando um sistema possui vários elétrons, estes ocuparão níveis de energia maiores a medida que os níveis inferiores estejam preenchidos.

A energia de Fermi é um conceito que tem muitas aplicações na teoria dos orbitais atômicos, no comportamento dos semicondutores e na física do estado sólido em geral.

Em física do estado sólido a superficie de Fermi é a superficie no espaço de momentos na qual a energia de excitação total se iguala à energia de Fermi. Esta superfície pode ter uma topologia não trivial. Simplificadamente se pode dizer que a superfície de Fermi divide os estados electrônicos ocupados dos que permanecem livres.

Enrico Fermi e Paul Dirac, derivaram as estatísticas de Fermi-Dirac. Estas estatísticas permitem predizer o comportamento de sistemas formados por um grande número de elétrons, especialmente em corpos sólidos.

A energia de Fermi de um gás de Fermi (ou gás de elétrons livres) não relativista tridimensional se pode relacionar com o potencial químico através da equação:

${\displaystyle \mu =\epsilon _{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{\epsilon _{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{\epsilon _{F}}}\right)^{4}+...\right]}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

onde ε_F é a energia de Fermi, k é a constante de Boltzmann e T é a temperatura. Portanto, o potencial químico é aproximadamente igual a a energia de Fermi à temperaturas muito inferiores a uma energia característica denominada Temperatura de Fermi, ε_F/k. Esta temperatura característica é da ordem de 10⁵K para um metal a uma temperatura ambiente de (300 K), pelo que a energia de Fermi e o potencial químico são essencialmente equivalentes. Este é um detalhe significativo dado que o potencial químico, e não a energia de Fermi, é quem aparece nas estatísticas de Fermi-Dirac.

Contexto avançado

Principais energias em estrutura de bandas para sólidos cristalinos.

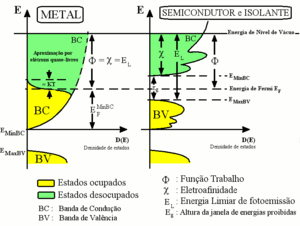
Elétrons são férmions, ou seja, são partículas regidas pela estatística de Fermi. Nesta estatística, um dado estado quântico pode ser ocupado por no máximo um e não mais que um férmion, e portanto a máxima probabilidade de ocupação de um dado estado quântico é um. Os elétrons situados dentro da amostra estão confinados por um potencial atrativo exercido pelos íons positivos da rede. Conforme mostrado pela mecânica quântica, potenciais confinantes apresentam níveis de energias discretos. No caso dos átomos isto se reflete nos tão conhecidos níveis atômicos de energia e no caso dos sólidos cristalinos, a aproximação entre os átomos leva a um agrupamento dos estados em bandas de energia. Estas bandas são vistas nas relações de dispersão para os sólidos como sendo as regiões de energia permitidas para os elétrons, separadas umas das outras por janelas de energias proibidas (ou “gaps”).

Rigorosamente falando,^[1] a energia do nível de Fermi é definida em sistemas à temperatura de zero absoluto. Nesse caso, a energia do nível de Fermi é a energia do nível mais energético ocupado, visto que nessa temperatura todos os níveis com energia menor que a energia do nível de Fermi estariam ocupados (probabilidade igual a 1) e todos os níveis com energia acima, desocupados (probabilidade de ocupação nula). Para sistemas em temperaturas não nulas, não temos mais uma transição abrupta da probabilidade de ocupação, e sim uma probabilidade dada pela distribuição de Fermi-Dirac. Considera-se então como a energia do nível de Fermi a energia obtida pela média aritmética ponderada das energias de cada estado energético afetado pela excitação térmica (estados com probabilidades de ocupação diferentes de 1 ou 0) pesadas cada qual pela respectiva probabilidade de ocupação do estado associado. O denominador desta média será obviamente o número de estados envolvidos no processo. Repare que em acordo com a estatística de Fermi, dentre os referidos estados os menos energéticos têm probabilidade de ocupação maior do que aqueles mais energéticos. Para aproximação de elétrons livres a densidade de estados cresce com a raiz quadrada da energia, resultando em uma parábola no gráfico de energia x densidade de estados. Em semicondutores e isolantes esta dependência pode ser bem mais complicada.

Outra definição equivalente implica dizer que a energia de Fermi corresponde ao potencial eletroquímico do sistema na temperatura de zero absoluto. Uma extensão a temperaturas maiores é evidente, e a energia de Fermi corresponde assim ao potencial eletroquímico do sistema na temperatura considerada. A energia de Fermi expressa, portanto, qual seria a variação da energia interna total do sólido, considerado sempre como sistema isolado e em equilíbrio termodinâmico, caso um elétron fosse dele removido. Sendo E_N^total a energia total do sistema no estado neutro, em seu equilíbrio termodinâmico, e E_N-1^total a energia total do sistema também em seu novo equilíbrio termodinâmico mas após a remoção do elétron, temos que:

E_F = E_N^total - E_N-1^{total /} 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Nas definições acima, o nível de referência é o nível de menor energia disponível aos N elétrons, e a remoção de um elétron provoca, então, a redução da energia do sistema. Neste referencial a energia de Fermi é, portanto, positiva, bem como o potencial eletroquímico.

Quando dois materiais diferentes são colocados em contato, a condição de equilíbrio termodinâmico exige que as suas energias de Fermi sejam iguais. Se as energias de Fermi fossem diferentes, a passagem de um elétron do sólido com maior energia de Fermi para o sólido com menor energia de Fermi resultaria em uma diminuição da energia total do sistema e o sistema composto não estaria, então, em sua configuração de equilíbrio, a de mínima energia, conforme exigido pelas leis da termodinâmica. Este fato dá origem a um fenômeno conhecido por diferença de potencial de contato que encontra diversas aplicações práticas, a saber na eletrônica de estado sólido (junção PN) e no uso do metal de sacrifício em navios.

Ilustração do conceito para compartimento monodimensional quadrado

A monodimensional compartimento quadrado infinito é um modelo para uma caixa mono dimensional. É um sitema modelo padrão em mecânica quântica para o qual a solução para uma partícula isolada é bem conhecido. Os níveis são marcados por um único número quântico n e as energias são dadas por

${\displaystyle E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}\,}$. / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Suponha-se agora que em vez de uma partícula nesta caixa nós temos N partículas na caixa e que estas partículas são férmions com spin 1/2. Então somente duas partículas podem ter a mesma energia i.e. duas partículas podem ter a energia de ${\displaystyle E_{1}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}}$, /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..ou duas partículas podem ter energia  e assim por diante. A razão que duas partículas podem ter a mesma energia é que uma partícula de spin 1/2 pode ter um spin de 1/2 (spin "acima") ou um spin de -1/2 (spin "abaixo"), conduzindo a dois estadois para cada nível de energia. Quando nós olhamos na energia total deste sistema, a configuração para as quais a energia total é a menor (o estado fundamental), é a configuração onde todos os níveis de energia acima de n=N/2 estão ocupados e todos os níveis mais altos estão vazios. A energia de Fermi é consequentemente

${\displaystyle E_{f}=E_{N/2}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}(N/2)^{2}\,}$. / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

O caso tridimensional

O caso tridimensional isotrópico é conhecido como a esfera de Fermi.

Deixe-nos agora considerar uma caixa cúbica tridimensional que tem um lado de comprimento L (ver compartimento quadrado infinito). Este torna-se uma muito boa aproximação para descrever elétrons em um metal.

Os estados agora são marcados po três números quânticos n_x, n_y, e n_z. As energias da partícula isolada são

${\displaystyle E_{n_{x},n_{y},n_{z}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

n_x, n_y, n_z são inteiros positivos.

Existem múltiplos estados com a mesma energia, por exemplo ${\displaystyle E_{100}=E_{010}=E_{001}}$. Agora deixemos colocar-se N férmions não interativos de spin 1/2 nesta caixa. Para calcular a energia de Fermi, nós veremos no caso de que N é grande.

Se nós introduzios um vetor ${\displaystyle {\vec {n}}=\{n_{x},n_{y},n_{z}\}}$ então cada estado quântico corresponde a um ponto num "n-espaço" com energia

${\displaystyle E_{\vec {n}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}|{\vec {n}}|^{2}\,}$. / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

O número de estados com energia menor que E_f é igual ao número de estados que residem em uma esfera de raio ${\displaystyle |{\vec {n}}_{f}|}$ na região do "n-espaço" onde n_x, n_y, n_z são positivos. No estado básico este número iguala o número de férmions no sistema.

${\displaystyle N=2\times {\frac {1}{8}}\times {\frac {4}{3}}\pi n_{f}^{3}\,}$

Os três férmions que ocupam os mais baixos estados de energia formam uma esfera em espaço de momento. A superfície desta esfera é a superfície de Fermi.

o fator é de dois é novamente porque são doisestados de spin, o fator de 1/8 é porque somente 1/8 da esfera repousa na região onde todos n são positivos.

Nós obtemos

${\displaystyle n_{f}=\left({\frac {3N}{\pi }}\right)^{1/3}}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

então a energia de Fermi é dada por

${\displaystyle E_{f}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{f}^{2}}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

${\displaystyle ={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{2/3}}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Tais resultados em uma relação entre a energia de Fermi e o número de partículas por volume (quando nós substituímos L² com V^2/3):

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N}{V}}\right)^{2/3}\,}$

 / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

A energia de Fermi total de um esfera de fermi de ${\displaystyle N_{0}}$ férmions é dada por

${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={3 \over 5}N_{0}E_{f}}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={\int _{0}}^{N_{0}}{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{\frac {2}{3}}dN}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

${\displaystyle ={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}{\int _{0}}^{N_{0}}N^{\frac {2}{3}}dN={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}\left({\frac {3}{5}}N_{0}^{\frac {5}{3}}\right)={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Energia de Fermi total:

${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

 / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Integração por substituição:

${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}={\frac {3}{5}}N_{0}\left[{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N_{0}}{\pi }}\right)^{2/3}\right]={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}}$

A eliminação de ${\displaystyle L}$ em favor de ${\displaystyle V}$:

${\displaystyle L^{2}=V^{\frac {2}{3}}}$

${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}N_{0}^{\frac {5}{3}}}{10mV_{0}^{\frac {2}{3}}}}}$

 / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Energias de Fermi típicas

Anãs brancas

Estrelas conhecidas como anãs brancas tem massa comparável a nosso Sol, mas têm um raio aproximadamente 100 vezes menor. As alta densidades implicam que os elétrons estão não mais ligados a um núcleo isolado e formam um gás de elétrons degenerado. Os números da densidade de elétrons em uma anã branca são da ordem de 10³⁶ elétrons/m³. Isto significa que sua energia de Fermi é:

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{e}}}\left({\frac {3\pi ^{2}(10^{36})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{5}\ \mathrm {eV} \,}$/ 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Núcleos

Outro exemplo típico é as partículas em um núcleo de um átomo. Os núcleons de um núcleo atômico pode ser tratado, assim, como um gás de Fermi e como tal, modelado.^[2]

O raio do núcleo é aproximadamente^[3]:

${\displaystyle R=\left(1.25\times 10^{-15}\mathrm {m} \right)\times A^{1/3}}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

onde A é o número de núcleons.

O número densidade de núcleons em um núcleo é conseqüentemente:

${\displaystyle n={\frac {A}{{\begin{matrix}{\frac {4}{3}}\end{matrix}}\pi R^{3}}}\approx 1.2\times 10^{44}\ \mathrm {m} ^{-3}}$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Agora, como a energia de fermi somente aplica-se a férmions de mesmo tipo, deve-se dividir esta energia por dois. Isto por causa da presença de nêutrons que não afetam a energia de Fermi dos prótons no núcleo, e vice versa.^[4][5][6]

Assim a energia de fermi de um núcleo é dada por:

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{p}}}\left({\frac {3\pi ^{2}(6\times 10^{43})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 30\times 10^{6}\ \mathrm {eV} =30\ \mathrm {MeV} }$ / 

 G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

O raio do núcleo admite desvios em torno do valor mencionado acima, então um típico valor para a energia de Fermi normalmente dada é 38 MeV.

 /  G ψ = E ψ = Eψ ω Mom=   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

uma função gaussiana típica usada na análise de espectros XPS: os parâmetros A₀, A₁, X_c e W são ajustados pelo programa de análise de forma que a curva ajuste-se da melhor forma possível aos dados experimentais.